I fisici creano il labirinto più complesso del mondo per domare i cristalli alieni

Usando gli scacchi e la geometria frattale per comprendere la struttura di un tipo di cristallo particolarmente strano, i fisici britannici e svizzeri hanno progettato un algoritmo che si è dimostrato capace di produrre un labirinto di assoluta complessità diabolica – il più difficile di tutti, secondo loro.

Le cose su cui sta lavorando questa squadra in realtà non sono cristalli in senso stretto: sono in realtà cristalli Semicristo. A differenza dei cristalli normali che sono incredibilmente abbondanti, esistono anche i quasicristalli Eccezionalmente raro allo stato naturale. In effetti, ci sono solo poche fonti naturali conosciute, tutte meteoriti.

A parte la loro rarità, ciò che rende questi materiali così interessanti è la loro architettura. Gli atomi sono disposti in una struttura altamente organizzata e coordinata, come i cristalli convenzionali. Ma a differenza di quest’ultimo, I gruppi atomici non si ripetono periodicamente nello spazio seguendo uno schema semplice. Invece, mostrano tipi di simmetria più dettagliati.

« I quasicristalli hanno tutte queste simmetrie che non possono essere trovate nei cristalli, il che è molto interessante. È una branca della matematica molto bella, ma chiunque può apprezzarne la bellezza direttamente, senza doverne comprendere i dettagli. », spiega Felix Flicker, coautore dello studio da lui citato nuovo mondo.

Cristallo, scacchi e matematica

Dato che ci sono così tanti esempi, la scienza ha ancora molto da imparare sulle proprietà dei quasicristalli. Per comprendere meglio questi alieni geometrici, il team di Flicker ha deciso di creare un algoritmo altamente specializzato per descriverne la struttura. Per raggiungere questo obiettivo, si sono ispirati… al fallimento.

La relazione non è chiara, ma la struttura quasicristallina introduce idiosincrasie con un antico problema logico basato sui movimenti dei pezzi più unici nel re dei giochi da tavolo.

dice questo indovinello Il cavaliere di Eulero Si inizia con un cavaliere posizionato su qualsiasi casella del tabellone. L’obiettivo è fargli visitare tutte le altre scatole senza passare due volte nella stessa scatola. Quando tracciamo il percorso di questo passeggero, otteniamo ciò che chiamiamo a Circuito di HamiltonCiò significa che attraversa tutti i punti del grafico una sola volta.

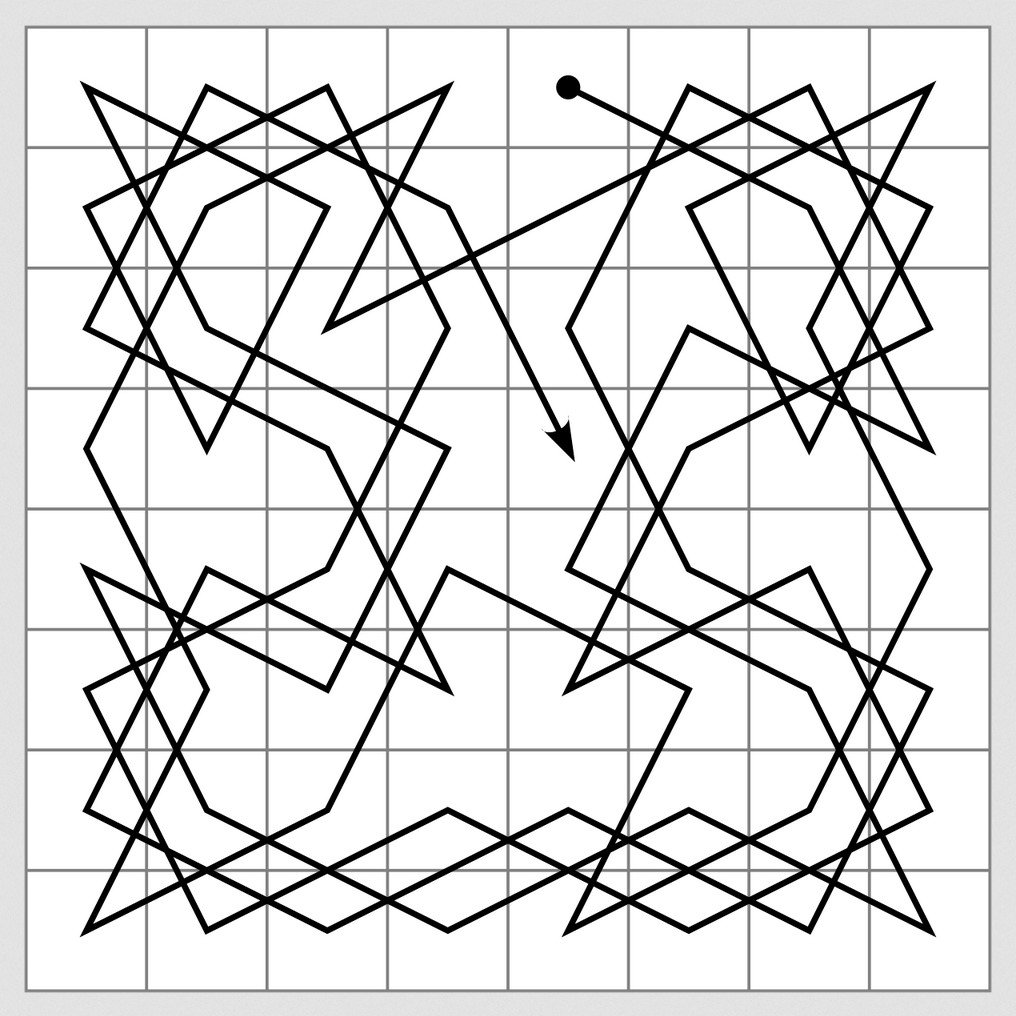
Tuttavia, è stato dimostrato che anche la struttura degli atomi nei quasicristalli segue questa regola. È qui che il lavoro diventa interessante, perché questa somiglianza ci consente di comprendere il problema dal punto di vista della teoria della complessità.

Un’incursione nella teoria della complessità

In generale, trovare il cerchio hamiltoniano è ciò che chiamiamo a Un problema NP-completo. Con questo termine si indica un problema la cui complessità aumenta esponenzialmente con il numero dei componenti, al punto che diventa presto impossibile calcolarne la soluzione con la forza bruta sulla nostra scala temporale. D’altra parte, se ci troviamo di fronte a una possibile soluzione, è facile verificare velocemente se è corretta, proprio come in un puzzle in cui dobbiamo solo osservare l’immagine finale.

Quindi la sfida consiste nel trovare un modo per risolvere i cosiddetti problemi NP-completi in tempi ragionevoli (o più precisamente nel cosiddetto tempo polinomiale). È un problema che fa impazzire i matematici da decenni. In effetti, rientra addirittura nel raggio d’azione r=nbuno di quelli famosi Problemi del Premio del Millennio. Questo è un elenco di sette principali problemi di matematica con un premio di 1 milione di dollari. Finora solo uno di loro, ovvero… Congettura di Poincarérisolto (da Grigory Perelman nel 2010).

Questa equazione incarna una domanda quasi esistenziale per i matematici: Questi problemi complessi sono davvero così difficili da affrontare come sembrano, oppure esiste una soluzione generale semplice che nessuno ha ancora trovato in modo da poter trovare rapidamente una soluzione?

Se questa ipotesi P=NP dovesse mai essere confermata, il che non è del tutto certo, Gli effetti saranno enormi. Ciò cambierebbe radicalmente la natura di una serie di problemi molto importanti per la scienza moderna, ma che oggi sono considerati quasi insolubili (vedi il nostro articolo qui sotto per maggiori dettagli).

Il punto è che tutti i teorici della complessità concordano su un punto: sostengono che se esiste un algoritmo per risolvere un singolo problema NP-completo in tempo ragionevole (polinomiale), allora Ciò significa che esiste una soluzione relativamente semplice anche per tutti gli altri problemi NP-completiCompresi i circuiti Hamilton! Molti di essi si sono rivelati di eccezionale importanza per la scienza moderna. Possiamo menzionare Il problema del commesso viaggiatorela cui rapida soluzione eliminerebbe immediatamente molti problemi logistici molto difficili, o Meccanismi di ripiegamento delle proteine Quali team di DeepMind hanno elaborato utilizzando l’apprendimento automatico.

Ora, si scopre che il cavaliere Eulero lo è Caso speciale. Sebbene i circuiti hamiltoniani siano generalmente problemi NP-completi, ce ne sono alcuni che possono essere risolti rapidamente utilizzando un po’ di ingegno matematico. Knight Euler è uno di questi: possiamo trovare velocemente la soluzione utilizzando un metodo semplice, Algoritmo di Warnsdorf. Poiché questo problema è strettamente correlato alla struttura dei quasicristalli, gli autori di questo lavoro hanno cercato un metodo simile da applicare al proprio problema.

E ne hanno trovato uno, che ha permesso loro di creare questo labirinto molto difficile che mostra la disposizione degli atomi in questi materiali.

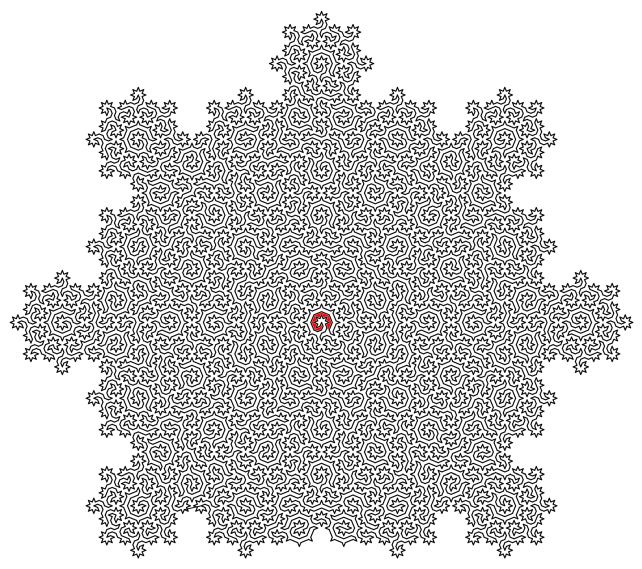
Non una prova di P=NP, ma interessanti applicazioni concrete

Secondo quanto riferito dai ricercatori Avviso scientificoQuesto lavoro potrebbe avere implicazioni molto tangibili in settori quali l’ottica o la cattura del carbonio.

D’altra parte, ciò non significa affatto che il problema dei circuiti hamiltoniani sia risolto una volta per tutte; Per quanto riguarda il cavaliere di Eulero, è semplicemente una domanda Un modo molto elegante per semplificare un problema molto specifico e non rappresenta affatto una soluzione generale.

Pertanto, non è nemmeno una risposta all’ipotesi P=NP e a tutte le altre domande NP-complete… ma forse è un passo in quella direzione. chi lo sa ; Se mai emergesse una soluzione rigorosa, questo lavoro potrebbe essere ricordato come uno dei pezzi che aprirono la strada a una delle rivoluzioni più importanti nella storia della matematica.

Il testo dello studio è disponibile Qui.

🟣 Per non perdere nessuna novità su Journal du Geek, iscriviti a Google News. E se ti piacciamo, abbiamo una newsletter ogni mattina.